Tree Traversal
트리 t의 traversal이란 각 노드를 정확힌 1번씩만 iterate(방문)하는 알고리즘을 말한다.
Note; 이 포스트에서 아래의 4가지 traversal알고리즘은 트리(특히 이진트리)구조에만 예시로 적용되어 있는데, 사실 트리의 상위 개념인 그래프구조에(노드와 엣지가 존재하는) 적용할 수 있다.
InOrder Traversal
inorder traversal은 left subtree - root - right subtree 순서로
recursive(재귀적)하게 iterate하며 처리하는 알고리즘이다. 기본적인 수도코드는 아래와 같다.
inOrder(t) {
if(t is not empty) {
inOrder( left subtree of t )
process t's root element
inOrder( right subtree of t )
}
}
PostOrder Traversal
postorder traversal은 left subtree - right subtree - root 순서로
recursively iterate하며 처리하는 알고리즘이다. 기본적인 수도코드는 아래와 같다.
postOrder(t) {
if(t is not empty) {
postOrder( left subtree of t )
postOrder( right subtree of t )
process t's root element
}
}
PreOrder Traversal (DFS)
preorder traversal은 root - left subtree - right subtree 순서로
recursively iterate하며 처리하는 알고리즘이다. 기본적인 수도코드는 아래와 같다.
preOrder(t) {
if(t is not empty) {
process t's root element
preOrder( left subtree of t )
preOrder( right subtree of t )
}
}
Level-Order Traversal (BFS)
level-order traversal은
root - roots of children(from left to right) - roots of grandchildren(from left to right) - … 순서로
recursively iterate하며 처리하는 알고리즘이다. 기본적인 수도코드는 아래와 같다.
levelOrder(BinaryTree t) {
if(t is not empty) {
// enqueue current root
queue.enqueue(t)
// while there are nodes to process
while( queue is not empty ) {
// dequeue next node
BinaryTree tree = queue.dequeue();
process tree's root;
// enqueue child elements from next level in order
if( tree has non-empty left subtree ) {
queue.enqueue( left subtree of t )
}
if( tree has non-empty right subtree ) {
queue.enqueue( right subtree of t )
}
}
}
}
적용
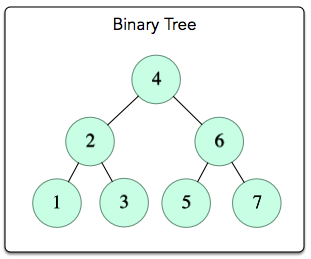
위의 그림에 4가지 traversal알고리즘을 적용하면 아래와 같이 처리한다.
- InOrder:
1 2 3 4 5 6 7 - PostOrder:
1 3 2 5 7 6 4 - PreOrder:
4 2 1 3 6 5 7 - Level-Order:
4 2 6 1 3 5 7