Binary Tree
Binary Tree(이진트리)는 기본적으로 노드와 엣지로 구성된다. 이진트리는 노드가 없거나 또는 두개의 child 노드를(left subtree와 right subtree) 갖는 하나의 root 노드로 구성된다. 이진이라는 이름에서 알 수 있듯이 이진트리는 최대 2개의 자식들을 갖는다.
- Binary Tree의 Top노드를 root라고 한다.
- 하나의 노드는 left, right subtree를 갖고, 이를 children이라 한다. 이때 그 노드를 parent라고 한다.
- root노드가 아니면서 children이 없는 노드를 leaf노드라고 한다.
- 노드 a가 노드 b의 ancestor라는 것은 노드 b가 노드 a의 left 또는 right subtree안에 위치한다는 것이다.
- 따라서, Binary Tree안에서 root노드는 다른 모든 노드의 ancestor가 된다.
- 노드 a의 depth(또는 level)는 root노드로 부터의 거리, 즉 엣지의 갯수를 의미한다.
- 트리의 height는 root노드와 가장 먼 leaf노드와의 엣지의 갯수를 의미한다. root노드 r을 갖는 이진트리 t의 height는 다음과 같다. height(t) = 1 + max(height(r.leftchild), height(r.rightchild))
이 개념을 아래 그림에 적용해보자.
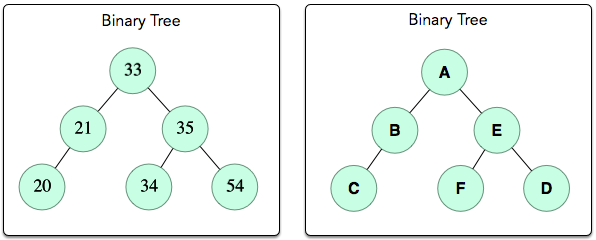
- Binary Tree의 root노드는 A이다.
- A의 children노드는 B와 E이고, B와 E의 parent노드는 A이다.
- C, F, D는 leaf노드들이다.
- B는 C의 parent이며, ancestor이다.
- A는 다른 모든 노드인 B~F의 ancestor이다.
- depth(또는 level)는 root노드 A로부터의 엣지의 갯수이다. 따라서 A의 depth는 0이고, B, E의 depth는 1이다.
- height는 다음 재귀식을 따른다. height(t) = 1 + max(height(r.leftchild), height(r.rightchild))
= 1 + max(height(A.leftchild), height(A.rightchild))
= 1 + max(height(B), height(E))
= 1 + max((1 + max(height(B.leftchild), height(B.rightchild))), (1 + max(height(E.leftchild), height(E.rightchild))))
= 1 + max((1 + max(height(C), height(None))), (1 + max(height(F), height(D))))
= 1 + max((1 + max(height(C), height(None))), (1 + max(height(F), height(D))))
…
= 1 + max((1 + max(0, -1)), (1 + max(0, 0)))
= 1 + max((1 + 0), (1 + 0))
= 1 + max(1, 1)
= 1 + 1 = 2
Binary Search Tree
Binary Search Tree(이진검색트리)는 Binary Tree의 조건을 모두 만족하면서, 아래의 3가지 조건을 추가적으로 만족하는 Tree것을 말한다. BST는 BT를 검색을 위해 사용하는 자료구조이다.
- 이진트리 t의 left subtree에 포함되는 모든 노드들은 t의 root노드의 값보다 작거나 같다.
max(leftTree(t).value <= t.value) - 이진트리 t의 right subtree에 포함되는 모든 노드들은 t의 root노드의 값보다 크다.
max(rightTree(t).value > t.value) - leftTree(t), rightTree(t)는 모두 BST들이다.