문제



풀이 및 답
처음에는 shortest path하길래 무조건 다익스트라 알고리즘을 쓰면 되겠거니 했다. 주입식교육이란.. 그런데 문제의 BFS를 보고나서 다익스트라 말고, BFS 방법으로 풀어보려고 시도했다.
class Graph:
def __init__(self, n):
self.nodes = n
self.edges = [[0] * n for _ in range(n)]
def connect(self, from_node, to_node):
self.edges[from_node][to_node] = 1
self.edges[to_node][from_node] = 1
def find_all_distances(self, node):
from queue import Queue
distances = [-1] * n
queue = Queue()
queue.put((node, -1, 0))
while not queue.empty():
_node, _prev_node, _distance = queue.get()
distances[_node] = _distance
for idx, edge in enumerate(self.edges[_node]):
if not idx == _prev_node and edge:
queue.put((idx, _node, _distance+1))
return [6*d if d != -1 else d for d in distances]
t = int(input())
for i in range(t):
n,m = [int(value) for value in input().split()]
graph = Graph(n) # O(n)
for i in range(m): # O(m)
x,y = [int(x) for x in input().split()]
graph.connect(x-1,y-1)
s = int(input())
distances_from_s = graph.find_all_distances(s-1) # O((n-1)^2)
print(' '.join([str(distance) for distance in distances_from_s if distance != 0]))
초기 완성 코드는 위와 같았다. 케이스 7개 중 4개에서 timeout이 떴다. 로직에 문제가 있는건가 잠깐 생각하다가, hackerrank는 테스트케이스의 input, output을 볼 수 있어서
먼저 살펴본 결과, input의 n(node 숫자), m(edge 숫자)이 충분히 클 때 timeout이 발생하는 것으로 보여 우선 time complexity를 파악해봤다.
우선 Graph class의 __init__함수에서 인라인 for문 O(n),
edge를 연결하기 위한 connect함수가 호출되는 횟수가 O(m),
distance를 계산하기 위한 find_all_distances함수에서 queue가 empty일때까지 반복하는 루프는 worst case가 fully connected graph일 경우 O((n-1)^2)
이고, 따라서 O(n) + O(m) + O((n-1)^2)을 계산해보려 하던 찰나…..
이 생각의 흐름속에서 fully connected graph일 경우를 간단한 케이스로 생각해보았을 때 위의 로직으로는 무한루프에 빠진다는 것을 알게 됐다. 잠깐 생각했던 로직에 문제가 있던 것이 맞았다.
역시 의심할 것은 내 머리, 내가 짠 로직이다.
아래와 같이 node가 3개인 fully connected graph를 생각해볼 경우, queueing이 반복된다.
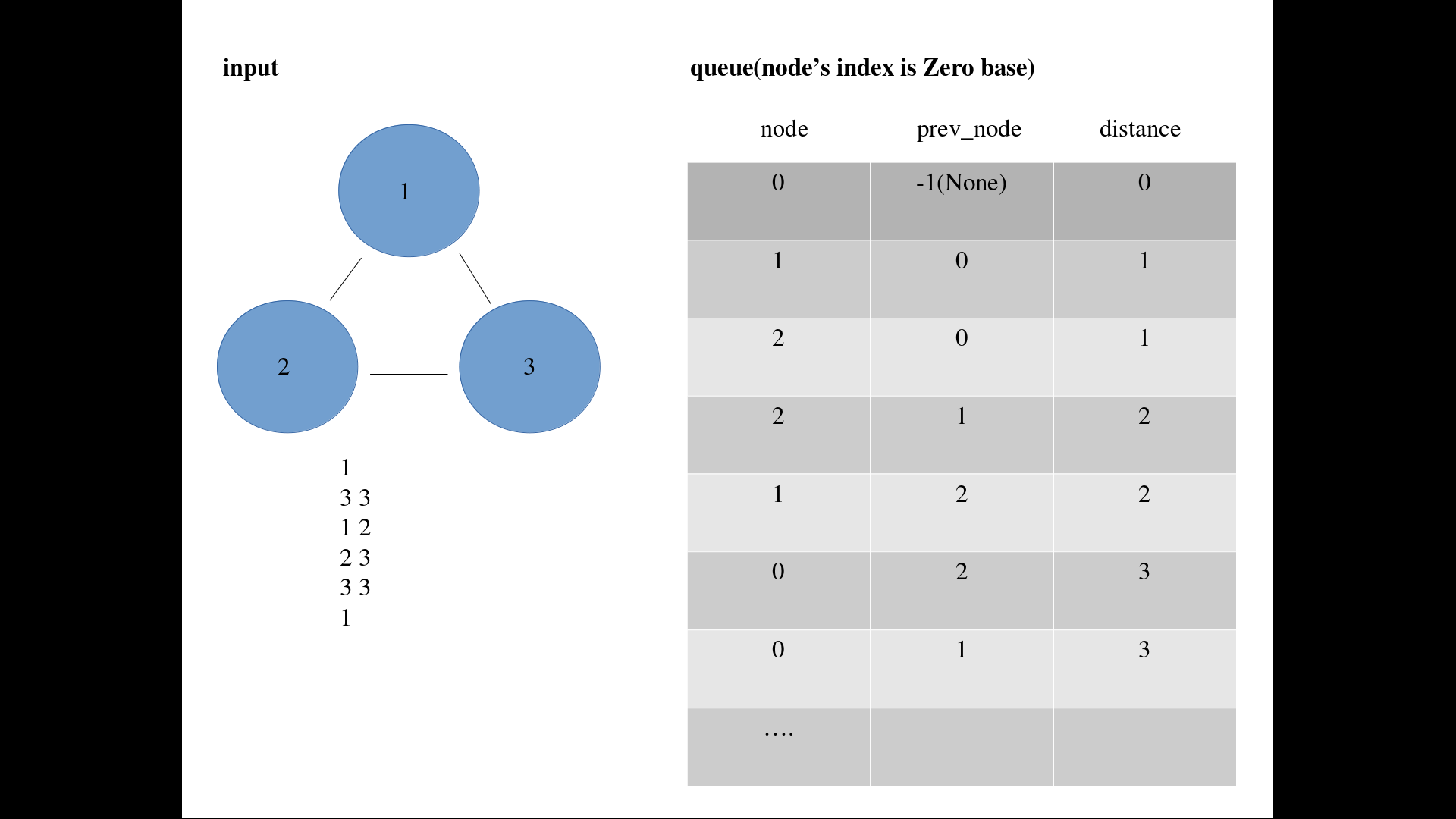
문제점을 파악한 후 아래와 같이 이미 distance가 구해져 있는 경우에는 값을 비교하여 더 작을 경우만 queueing 하도록 if문을 추가하여 문제를 해결했다.
class Graph:
def __init__(self, n):
self.nodes = n
self.edges = [[0] * n for _ in range(n)]
def connect(self, from_node, to_node):
self.edges[from_node][to_node] = 1
self.edges[to_node][from_node] = 1
def find_all_distances(self, node):
from queue import Queue
distances = [-1] * n
queue = Queue()
queue.put((node, -1, 0))
while not queue.empty():
_node, _prev_node, _distance = queue.get()
if distances[_node] == -1 or _distance < distances[_node]:
distances[_node] = _distance
for idx, edge in enumerate(self.edges[_node]):
if not idx == _prev_node and edge:
queue.put((idx, _node, _distance+1))
return [6*d if d != -1 else d for d in distances]
t = int(input())
for i in range(t):
n,m = [int(value) for value in input().split()]
graph = Graph(n)
for i in range(m):
x,y = [int(x) for x in input().split()]
graph.connect(x-1,y-1)
s = int(input())
distances_from_s = graph.find_all_distances(s-1)
print(' '.join([str(distance) for distance in distances_from_s if distance != 0]))