Asymptotic Analysis(점근적 분석): A very limited overview.
어떠한 문제 해결을 위한 알고리즘의 성능분석을 할 때, 주어지는 데이터의 형태나 실험을 수행하는 환경, 또는 실험에 사용한 시스템의 성능등
다양한 요소에 의해 공평한 결과가 나오기 힘들고 비교 결과가 항상 일정하지 않을 수 있다.
이를 효과적으로 해결하는 방법이 점근적 분석법이다. 점근적 분석법은 각 알고리즘이 주어진 데이터의 크기를 기준으로 수행시간 혹은 사용공간이 얼마나 되는지를 객관적으로 비교할 수 있는 기준을 제시해 준다.
O(빅오), Ω(오메가), Θ(세타)등이 있다. 일반적으로 빅오와 세타표기가 많이 사용된다.
O Notation (빅오 표기법)
- 점근적 상한선(Asymptotic upper bound)
- 주어진 알고리즘이 아무리 나빠도 비교하는 함수와 같거나 좋다.
(= 주어진 알고리즘이 비교하는 함수보다 수행시간이 짧다, 주어진 알고리즘이 비교하는 함수보다 좋다.) - 정의 :
O(g(n)) = {f(n) : there exist positive constants c and n0 such that 0≤f(n)≤cg(n) for all n≥n0}
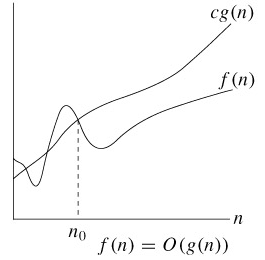
n0를 기준으로 n0보다 오른쪽에 있는 모든 n 값에 대해 함수 f(n)은 함수 cg(n)보다 작거나 같다는 의미이다. 그래프가 아래에 있을 수록 수행시간이 짧은 것이므로 성능이 좋은 것이다.
Ω Notation (오메가 표기법)
- 점근적 하한선(Asymptotic lower bound)
- 주어진 알고리즘이 아무리 좋아도 비교하는 함수와 같거나 나쁘다.
(= 주어진 알고리즘이 비교하는 함수보다 수행시간이 길다, 오래걸린다, 주어진 알고리즘이 비교하는 함수보다 나쁘다.) - 정의 :
Ω(g(n)) = {f(n) : there exist positive constants c and n0 such that 0≤cg(n)≤f(n) for all n≥n0}
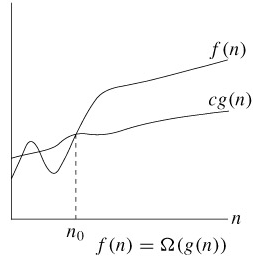
n0를 기준으로 n0보다 오른쪽에 있는 모든 n 값에 대해 함수 f(n)은 함수 cg(n)보다 크거나 같다는 의미이다.
Θ Notation (세타 표기법)
- 점근선 상한선과 점근적 하한선의 교집합(Asymptotic tighter bound)
- 주어진 알고리즘이 아무리 좋아지거나 나빠지더라도 비교하는 함수의 범위안에 있다.
- 정의 :
Θ(g(n)) = {f(n) : there exist positive constants c1, c2 and n0 such that 0≤c1g(n)≤f(n)≤c2g(n) for all n≥n0}
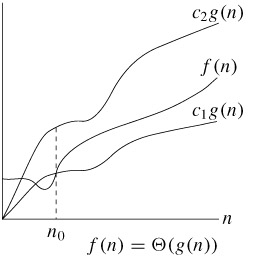
n0를 기준으로 n0보다 오른쪽에 있는 모든 n 값에 대해 함수 f(n)은 함수 c1g(n)보다 크거나 같거나 c2g(n)보다 작거나 같다는 의미이다.
Note; Θ(1) == O(1) == constant time
연산시간이 상수만큼의 시간을 필요로 하는 알고리즘을 표시할때 쓰이는 표기법이다.
적용
기본적으로 n개의 데이터가 주어졌을 때 best & worst scenario를 고려하며 upper & lower bound 함수(빅오 & 오메가)를 정해야한다.
일반적으로 상한선인 빅오 표기법만 계산한다.
for(int i = 0; i < n; i++) {
for(int j = 0; j < n/2; j++) {
// Θ(1) operation
// Θ(1) operation
// Θ(1) operation
}
}
위 코드에서 중첩 루프 안에 있는 3개의 상수 연산이 n*n/2 번 실행된다. 따라서, f(n) = 3*n*n/2 = 3/2*n^2 이므로, 시간복잡도는 O(n^2)이다.
Reference
Day 25: Running Time and Complexity
[컴퓨터 알고리즘 성능분석] 점근적 표기법 (Asymptotic Notation)